摘要
本文提出了一种高效且统一的框架,即ThiNet,来实现CNN网络模型在训练与预测阶段的同时加速与压缩。我们关注于滤波器级别的剪枝,即当某个滤波器的性能表现较弱时,该滤波器将被全部丢弃。我们的算法不改变原网络结构,因此可无缝适配于现有的深度学习框架。有别于已有的剪枝算法,我们将滤波器剪枝操作形式化地定义为一个优化问题,通过下一层的统计信息来指导当前层的剪枝。实验结果验证了该算法的有效性,ThiNet超过了现有的剪枝算法。同时,我们也在ILSVRC-12数据集上验证了ThiNet的性能。该算法在VGG16上能够降低3.31$\times$的FLOPs,16.63$\times$的网络参数,而top-5准确度下降仅为0.52%。在ResNet-50上的类似实验证明,即便是对于紧凑的网络,ThiNet也能减少超过一半的的参数与FLOPs,而top-5仅降低1%。此外,ThiNet甚至能将VGG16网络模型剪枝到只有5.05MB的大小,保留AlexNet级别的精度,却拥有更强的泛化性能。
1. 概览
1.1 ThiNet框架

图 1. ThiNet剪枝框架. 首先,我们根据图中的虚线框部分来判断哪些通道及其相对应的滤波器的性能较弱(第一行中用黄色高亮的部分)。这些通道(及其对应的滤波器)对网络的性能影响较小,因此可被丢弃,从而得到一个剪枝的模型。最后剪枝后的模型将被微调以恢复其精度。
1.2 收集训练样本
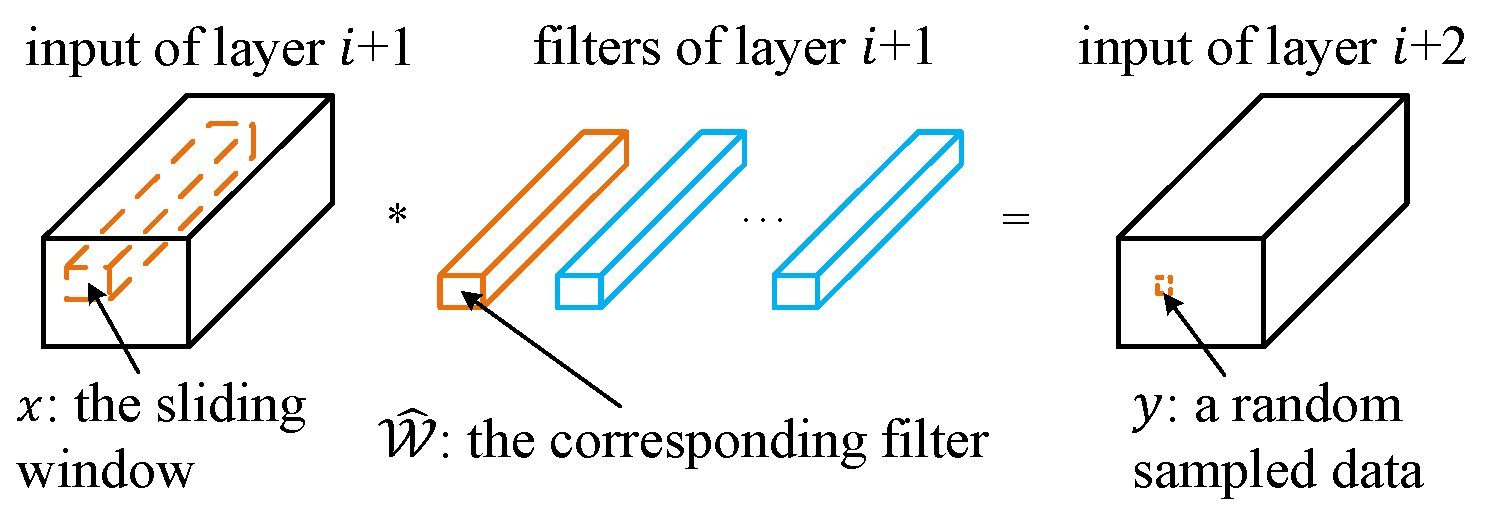
通常而言,带偏置项$b$的卷积计算如下所示:
\begin{equation}
y = \sum_{c=1}^C\sum_{k_1=1}^K\sum_{k_2=1}^K\widehat{\mathcal{W}}_{c,k_1,k_2}\times x_{c,k_1,k_2}+b
\end{equation}
现在,如果我们定义:
\begin{equation*}
\hat{x}_c=\sum_{k_1=1}^K\sum_{k_2=1}^K\widehat{\mathcal{W}}_{c,k_1,k_2}\times x_{c,k_1,k_2}
\end{equation*}
公式(1)便能简化为:\(\hat{y} = \sum_{c=1}^C\hat{x}_c\),这里 \(\hat{y} = y - b\)。 若我们能够找到一个通道子集\(S \subset \{1,2,\ldots, C\}\),使得下式
\begin{equation}
\hat{y} = \sum_{c \in S}\hat{x}_c
\end{equation} 成立,那么我们便能不再依赖于任何\(c \notin S\)的通道。因此,这些通道(及其对应的滤波器)便能在不改变CNN网络模型精度的前提下被安全移除。
当然,公式(2)不可能对于所有的\(\hat{x}\)与\(\hat{y}\)总保持成立。但我们可以手动提取一部分训练样本,来计算一个使得公式 (2) 近似正确的子集$S$。
1.3 一种用于通道选择的贪心算法
给定\(m\)($m$由图片数量与位置数量决定)个训练样本\(\{(\mathbf{\hat{x}}_i, \hat{y}_i)\}\),原通道选择问题可以转化为如下的优化问题:
\begin{equation}
\begin{aligned}
\mathop{\arg\min}\limits_{S} & \sum_{i=1}^{m}\left(\hat{y}_i-\sum_{j\in S}\mathbf{\hat{x}}_{i,j}\right)^2\\
\text{s.t.}\quad & |S|=C\times r, \quad S \subset \{1,2,\ldots, C\}.
\end{aligned}
\end{equation}
这里,\(|S|\)为子集$S$的元素数量,\(r\)为预定义的压缩率(即保留多少个通道)。令\(T\)为被移除的通道集合(\(S\cup T=\{1,2,\ldots,C\}\) 同时 \(S\cap T=\emptyset\)),我们便能最小化另一等价优化目标:
\begin{equation}
\begin{aligned}
\mathop{\arg\min}\limits_{T} & \sum_{i=1}^{m}\left(\sum_{j\in T}\mathbf{\hat{x}}_{i,j}\right)^2\\
\text{s.t.}\quad & |T|=C\times (1-r), \quad T \subset \{1,2,\ldots, C\}.
\end{aligned}
\end{equation}
公式(4)与公式(3)完全等价,但速度更快也更简单,因为$|T|$通常比$|S|$要小很多。求解公式(3)仍然是一个NP难的问题,因此我们提出了一种快速的贪心算法进行求解(算法1)。
1.4 最小化重构误差
在决定保留哪几个滤波器之后,我们可以通过对每一个通道赋予权重来进一步地减小重构误差:
\begin{equation}
\mathbf{\hat{w}}=\mathop{\arg\min}\limits_{\mathbf{w}}\sum_{i=1}^{m}(\hat{y}_i- \mathbf{w}^\mathrm{T}\mathbf{\hat{x}}^*_i)^2.
\end{equation}
公式 (5) 可以通过普通的最小二乘法来求解:$\mathbf{\hat{w}} = (\mathbf{X}^\mathrm{T}\mathbf{X})^{-1}\mathbf{X}^\mathrm{T}\mathbf{y}$.
2. 实验结果
2.1 不同的滤波器选择策略

图 3. 不同选择算法的性能比较:VGG-16-GAP模型以不同的压缩率在CUB-200数据集上的剪枝效果
2.2 VGG16在ImageNet上的表现
表 1. 使用ThiNet来对VGG-16在ImageNet上进行剪枝。这里,M/B表示百万/十亿($10^6$/$10^9$);f./b.是前向/反向的缩写,速度由batch size=32在一张M40 GPU上测试所得。
| Model | Top-1 | Top-5 | #Param. | #FLOPs | f./b. (ms) |
|---|---|---|---|---|---|
| Original1 | 68.34% | 88.44% | 138.34M | 30.94B | 189.92/407.56 |
| ThiNet-Conv | 69.80% | 89.53% | 131.44M | 9.58B | 76.71/152.05 |
| Train from scratch | 67.00% | 87.45% | 131.44M | 9.58B | 76.71/152.05 |
| ThiNet-GAP | 67.34% | 87.92% | 8.32M | 9.34B | 71.73/145.51 |
| ThiNet-Tiny2 | 59.34% | 81.97% | 1.32M | 2.01B | 29.51/55.83 |
| SqueezeNet [15] | 57.67% | 80.39% | 1.24M | 1.72B | 37.30/68.62 |
1为公平比较,原VGG-16模型是使用单张中心裁剪(先缩放至256$\times$256)的图片测试所得,该测试方法被广泛使用于[10, 14]。因此,由这种方法测试所得的准确度低于某些报告中的结果。
2组织ImageNet数据集时,通常有两种方法来对图像进行缩放:
为公平比较,我们依照前人工作,使用“固定大小”的方法来组织图像。但在实际应用中“保持长宽比”的算法更加实用。因此,我们使用该策略来训练ThiNet-Tiny模型。
- 固定大小: 每张图首先缩放至256$\times$256,再中心裁剪得到224$\times$224大小的区域;
- 保持长宽比: 每张图首先将短边缩放至256,再中心裁剪;
表 2. 与其他方法在VGG-16上的比较。部分工作的原文中未报告相关的准确数字,我们使用$\approx$来表示相应的近似值。
| Model | Top-1 | Top-5 | #Param. $\downarrow$ | #FLOPs $\downarrow$ |
|---|---|---|---|---|
| APoZ-1 [14] | -2.16% | -0.84% | 2.04$\times$ | $\approx$1$\times$ |
| APoZ-2 [14] | +1.81% | +1.25% | 2.70$\times$ | $\approx$1$\times$ |
| Taylor-1 [23] | - | -1.44% | $\approx$1$\times$ | 2.68$\times$ |
| Taylor-2 [23] | - | -3.94% | $\approx$1$\times$ | 3.86$\times$ |
| ThiNet-WS [21] | +1.01% | +0.69% | 1.05$\times$ | 3.23$\times$ |
| ThiNet-Conv | +1.46% | +1.09% | 1.05$\times$ | 3.23$\times$ |
| ThiNet-GAP | -1.00% | -0.52% | 16.63$\times$ | 3.31$\times$ |
3. 其他结果
3.1 剪枝过程的计算代价
我们的剪枝过程由两部分组成:特征提取与通道选择.
至于矩阵(用于通道选择的计算,见原文3.2.2节)的大小,当通道数为64时占用了51.2MB磁盘空间,而当通道数为512时,则占用了409.6MB。相比于微调和从头训练,这些计算代价微乎其微。
- 前者的计算速度取决于模型的预测速度,在M40上使用VGG-16花费了769.37s。
- 后者的计算速度由当前层的滤波器数量决定(conv1_1层是64,conv4_3层是512)。我们测试了这两层的计算时间,分别需要2.34s和137.36s来特征选择。
3.2 微调的作用
我们使用不同的选择算法来移除VGG-16-GAP模型中conv1_1层60%的滤波器(与4.1节相类似的实验设置),并对剪枝后的模型微调了1轮。其微调前后的精度变化(在CUB-200数据集上)如下所示:| Method | Before fine-tuning | After fine-tuning |
|---|---|---|
| random | 51.26% | 67.83% |
| weight sum [21] | 40.99% | 63.72% |
| APoZ [14] | 58.16% | 68.78% |
| ThiNet w/o w | 68.24% | 70.38% |
| ThiNet | 70.75% | 71.11% |
可见,微调对于恢复模型的准确度相当重要。同时,ThiNet表现出了相当鲁棒的性能。
4. 附加材料
我们提供额外的结果和必要的讨论:附加材料。
参考文献
Jian-Hao Luo, Jianxin Wu, and Weiyao Lin: ThiNet: A Filter Level Pruning Method for Deep Neural Network Compression
To appear in International Conference on Computer Vision (ICCV), 2017.
@inproceedings{iccv2017ThiNet,
title={{ThiNet: A Filter Level Pruning Method for Deep Neural Network Compression}},
author={Jian-Hao Luo, Jianxin Wu, and Weiyao Lin},
booktitle={International Conference on Computer Vision (ICCV)},
month={October},
year={2017}
}